All epidemiological biases are generally subsumed under three categories: uncontrolled confounding, selection bias, and information bias:
Confounding
Confounding can be thought of as the distortion of an exposure-outcome relationship due to external variables. More precisely, confounding occurs when the conditional expectation (E[Y|X=x]) differs from the controlled expectation (E[Y|do(X=x)]) in the marginal measures setting (parallels for the conditional measures setting exist). Confounding explains Simpson’s Paradox and led to Simpson’s conclusion that causal inference needs to be combined with statistical information in choosing between a marginal and conditional association measure.
Confounding as represented by a directed acyclic graph (DAG):
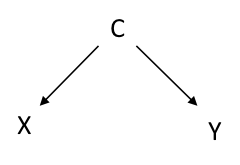
Key: X = exposure, Y = outcome, C = confounder.
Selection bias
Selection bias occurs when the observed association in those selected for analysis differs from the association in those who are eligible for analysis. This bias occurs in case-control studies when there is inappropriate selection of controls and occurs in cohort studies due to informative censoring. The key causal mechanism shared by all forms of selection bias is collider stratification, which involves conditioning on a variable, termed a collider, that is a shared common effect of two other variables.
DAG representing selection bias in case-control studies:
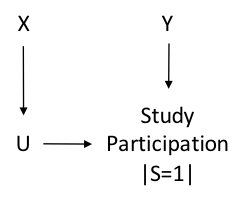
Key: X = exposure, Y = outcome, U = any variable that is caused by the exposure and affects selection.
DAGs representing selection bias in cohort studies:
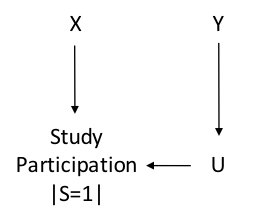
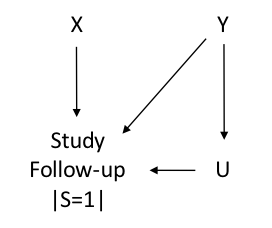
Key: X = exposure, Y = outcome, U = any variable that is caused by the outcome and affects (1) participation or (2) follow-up.
Information bias
Information bias can occur in epidemiological studies when the exposure, outcome, or both are incorrectly classified. This misclassification can be either independent or dependent, depending on whether the measurement error for the exposure is related to the measurement error of the outcome. Also, the misclassification can be either differential, if the measurement error of the exposure/outcome is affected by the outcome/exposure, or non-differential, if the measurement error of the exposure/outcome is not affected by the outcome/exposure.
DAGs representing different types of information bias:
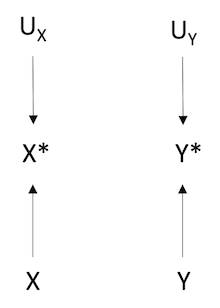independent, non-differential misclassification
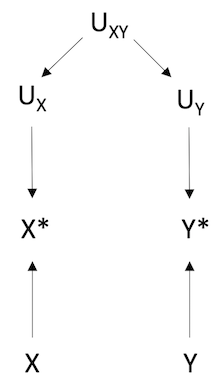dependent, non-differential misclassification
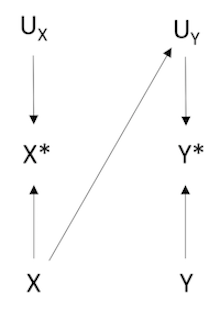independent, differential misclassification
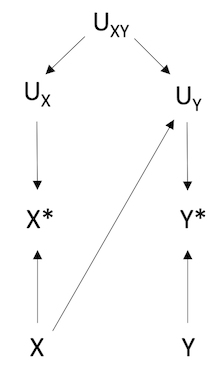dependent, differential misclassification
Key: X = true exposure, X* = misclassified exposure, UX = all factors other than X that determines the value of X, Y = true outcome, Y = misclassified outcome, UY = all factors other than Y that determines the value of Y*, UXY = factors affecting the measurement of both X and Y.